数学之美第二版
数学之美第二版读书笔记
3.1 用数学的方法描述语言规律
假定 S 表示一个有意义的句子,由一连串特定顺序排序的词 $w_1, w_2, … , w_n$ 组成,n 表示句子的长度。S 这个序列出现的概率等于每一个词出现的条件概率相乘。
其中,$P(w_1)$ 表示第一个词 $w_1$ 出现的概率。$P(w_2 \vert w_1)$ 表示在已知第一个词的前提下,第二个词出现的概率。
马尔科夫假设: 假设任意一个词 $w_i$ 出现的概率只同它前面的词 $w_{i-1}$ 有关。所以 S 出现的概率就变为:
这个公式对应的统计语言模型是二元模型 (Bigram Model)。
3.2.1 高阶语言模型
N-1 阶马尔科夫假设: 假设文本中的每个词 $w_i$ 与前面 N-1 个词有关。当前词 $w_i$ 的概率只取决于前面 N-1 个词。因此:
\(P(w_i|w_1, w_2, \cdot \cdot \cdot w_{i-1}) = P(w_i|w_{i-N+1}, w_{i-N+2}, \cdot \cdot \cdot, w_{i-1})\)
这个公式对应的语言模型称为 N 元模型 (N-Gram Model)。
马尔科夫假设的局限性: 在自然语言中,上下文之间的相关性可能跨度非常大,甚至可以从一个段落跨到另一个段落。因此,即使模型的阶数再提高,对这种情况也无可奈何。
3.2.2 模型的训练、零概率问题和平滑方法
使用语言模型需要知道模型中所有的条件概率,我们称之为模型的参数。通过对语料的统计,得到这些参数的过程称作模型的训练。
零概率或统计量不足问题: 对于二元模型来说,如果两个词 $ \# (w_{i-1}, w_i)$ 同现的次数为 0,那么条件概率 $P(w_i \vert w_{i-1}) = 0$。如果 $ \#(w_{i-1}, w_i)$ 和 $ \#(w_{i-1})$ 都只出现一次,那么 $P(w_i \vert w_{i-1}) = 1$。
如果用直接的比值计算概率,大部分条件概率是 0,这种模型我们称之为不平滑。
使用古德-图灵估计可以解决统计样本不足时的概率估计问题。原理为:对于没有看见的事件,我们不能认为它发生的概率为 0,因此我们从概率的总量中分配一个很小的比例给予这些没有看见的事件。
假定在语料库中出现 $r$ 次的词有 $N_r$ 个,特别地,未出现的词数量为 $N_0$,语料库的带下为 $N$,那么
\[N = \sum_{r=1}^\infty rN_r\]出现 $r$ 次的词在整个预料库中的相对频度则为 $r/N$。
假定 $r$ 比较小时,它的统计可能不可靠,因此出现 $r$ 次的那些词在计算它们的概率时要使用一个更小一点的次数,即 $d_r$:
\[d_r = (r + 1) \cdot N_{r+1}/N_r\]那么:
\[N = \sum_r d_r \cdot N_r\]一般来说,出现一次的词的数量比出现两次的多,出现两次的比出现三次的多,依此类推。这种规律称为 Zipf 定律。
在实际的自然语言处理中,一般对出现次数超过某个阀值的词,频率不下调,只对出现次数低于这个阀值的词,频率才下调,下调得到的频率总和给未出现的词。
对于出现 $r$ 次的词的概率估计为 $d_r/N$。所以,对于频率超过一定阀值的词,它们的概率估计就是它们在语料库中的相对频度,对于频率小于这个阀值的词,它们的概率估计就小于它们的相对频度,出现次数越少,折扣越多。对于未看见的词,也给予一个比较小的概率。这样所有词的概率估计都很平滑了。
估计二元模型概率的公式如下:
\[P(w_i|w_{i-1}) = \begin{cases} f(w_i|w_{i-1}) \,\,\,\qquad \, \#(w_{i-1}, w_i) \ge T \\ f_{gt}(w_i|w{i-1}) \quad \, 0 \lt \#(w_{i-1, w_i}) \lt T \\ Q(w_{i-1}) \cdot f(w_i) \,\,\, 其它 \end{cases}\]$T$ 是一个阀值,一般在 8 ~ 10 左右。
$f_{gt}$ 表示经过古德 - 图灵估计后的相对频度
\[Q(w_{i-1}) = \frac{1 - \sum\limits_{w_i \, seen} P(w_i|w_{i-1})}{\sum\limits_{w_i \, unseen} f(w_i)}\]没搞懂 $Q(w_{i-1})$ 为什么要这样计算
估计三元模型概率的公式如下:
\[P(w_i|w_{i-2}, w_{i-1}) = \begin{cases} f(w_i|w_{i-2}, w_{i-1}) \qquad \qquad \,\,\,\,\,\,\,\, \#(w_{i-2}, w_{i-1}, w_i) \ge T \\ f_{gt}(w_i|w_{i-2}, w_{i-1}) \qquad \qquad \quad 0 \lt \#(W_{i-2}, w_{i-1}, w_i) \lt T \\ Q(w_{i-2}, w_{i-1}) \cdot P(w_i|w_{i-1}) \quad 其它 \end{cases}\]5.2 隐含马尔可夫模型
在任何时刻 $t$,对应的状态 $S_t$ 都是随机的,任何一个状态 $S_t$ 的取值都可能与其它的状态相关。这样在随机的过程中就会有多个维度的不确定性。为了简化问题,做出了一种简化的假设,即随机过程中各个状态 $S_t$ 的概率分布,只与它前一个状态 $S_{t-1}$ 有关,即 $P(S_t \vert S_1, S_2, S_3, … , S_{t-1}) = P(S_t \vert S_{t-1})$ 。这个假设被命名为马尔可夫假设,而符合这个假设的随机过程则称为马尔可夫过程,或者称为马尔科夫链。
隐含马尔可夫模型是马尔科夫链的一个扩展:任何一个时刻 $t$ 的状态 $S_t$ 是不可见的。所以观察者没有办法通过观察到一个状态序列 $S_1, S_2, S_3, … , S_T$ 来推测转移概率等参数。但是,隐含马尔可夫模型在每个时刻 $t$ 会输出一个符号 $O_t$,而且 $O_t$ 和 $S_t$ 相关且仅和 $S_t$ 相关,这个被称为独立输出假设。
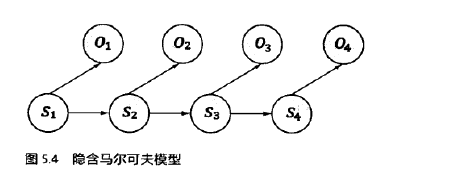
基于马尔可夫假设和独立输出假设,我们可以计算出某个特定的状态序列 $S_1, S_2, S_3, … $ 产生输出符号 $O_1, O_2, O_3, … $ 的概率。
\[P(S_1, S_2, S_3, ... , O_1, O_2, O_3, ...) = \prod_t P(S_t|S_{t-1}) \cdot P(O_t|S_t)\]贝叶斯定理:$P(A \vert B) = \frac{P(A) \cdot P(B \vert A)}{P(B)}$
5.3 延伸阅读:隐含马尔可夫模型的训练
转移概率:从前一个状态 $S_{t-1}$ 进入当前状态 $S_t$ 的概率 $P(S_t \vert S_{t-1})$。
生成概率:每个状态 $S_t$ 产生相应输出符号 $O_t$ 的概率 $P(O_t \vert S_t)$。
这些概率被称为隐含马尔可夫模型的参数,而计算或者估计这些参数的过程称为模型的训练。
训练隐含马尔可夫模型更实用的方式是仅仅通过大量观测到的信号 $O_1, O_2, O_3, … $ 就能推算模型参数的 $P(S_t \vert S_{t-1})$ 和 $P(O_t \vert S_t)$ 的方法,这类方法称为无监督的训练算法,其中主要使用鲍姆 - 韦尔奇算法。
6.1 信息熵
对于任意一个随机变量 $X$,它的熵定义如下:
\(H(X) = -\sum_{x \in X} P(x)logP(x)\)
log 表示以 2 为底
一条信息的信息量和它的不确定性有着直接的关系。变量的不确定性越大,熵也就越大,把它搞清楚所需要的信息量也就越大。
6.2 信息的作用
一个事物内部都会存在着随机性,也就是不确定性,假定为 $U$,而从外部消除这个不确定性唯一的办法是引入信息 $I$,而需要引入的信息量取决于这个不确定性的大小,即 $I > U$ 才行。当 $I < U$ 时,这些信息可以消除一部分不确定性。如果没有信息,那么无法排除不确定性。
对于两个随机变量 $X$ 和 $Y$,在 $Y$ 的条件下 $X$ 的条件熵定义为:
\[H(X|Y) = -\sum_{x \in X, y \in Y} P(x,y)logP(x|y)\]TODO 联合概率分布,条件概率分布
可以证明 $H(X) \ge H(X \vert Y)$。也就是说多了 $Y$ 以后,关于 $X$ 的不确定性下降了。等号成立说明增加了信息,不确定性却没有降低,当我们获取的信息和我们要研究的事物没有关系的时候,会出现这种情况。
11.1 搜索关键词权重的科学度量TF-IDF
关键词出现多的网页应该比它们出现较少的网页相关性高。但是有一个问题是,一般来说长网页包含的关键词要多些。所以,根据网页的长度,对关键词的次数进行归一化,也就是用关键词的次数除以网页的总字数。这个就是词频(Term Frequency,TF)。
但是还有一个问题是,停止词的词频很高,但是对确定网页的主题没有用处,所以在度量相关性时不应该考虑它的词频。
还有另一个问题是,不同词的重要程度应该要不一样。如果一个关键词只在很少的网页中出现,通过它可以很容易搜索到目标,它的权重应该大。反之,如果一个词在大量网页中出现,看到它仍然不很清楚要找什么内容,它的权重就应该小。
假定一个关键词$w$在$D_w$个网页中出现过,那么$D_w$越大,$w$的权重越小。反之亦然。使用逆文档频率(Inverse Document Frequency,IDF),公式为:$log(\frac{D}{D_w})$
$D$为全部网页数